共線形システムと例
の 共線ベクトル それらは3つのタイプの既存のベクトルのうちの1つです。それは、同じ方向または作用線にあるベクトルについてです。これは次のことを意味します。2つ以上のベクトルが互いに平行な直線上に配置されている場合、それらは共線になります。.
ベクトルは身体に適用される量として定義され、方向、感覚、スケールを持つものとして特徴付けられます。ベクトルは平面上または空間内で見つけることができ、異なるタイプにすることができます。つまり、共線ベクトル、同時ベクトル、並列ベクトルです。.

索引
- 1つの共線ベクトル
- 2つの特徴
- 2.1例1
- 2.2例2
- 2.3例1
- 3共線ベクトル系
- 3.1反対方向の共線ベクトル
- 3.2同じ意味の共線ベクトル
- 3.3大きさが等しく方向が反対の共線ベクトル
- 4共線形ベクトルと並行ベクトルの違い
- 5参考文献
共線ベクトル
各ベクトルのサイズと方向に関係なく、1つの作用線が他のすべてのベクトルの作用線とまったく同じである場合、それらのベクトルは同一線上にあります。.
ベクトルは、数学、物理、代数などのさまざまな分野での表現として、またジオメトリでも使用されます。ベクトルは、意味が異なるかどうかに関係なく、方向が同じ場合にのみ共線的になります。.
特徴
- 座標間の関係が等しい場合、2つ以上のベクトルが同一線上にある.
例1
ベクトルm = m_x; m_y、n = n_x; n_y。次の場合、これらは共線です。
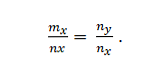
例2
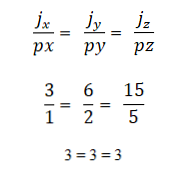
- 積またはベクトルの乗算がゼロ(0)に等しい場合、2つ以上のベクトルは同一線上にあります。これは、座標系では、各ベクトルはそれぞれの座標によって特徴付けられ、これらが互いに比例する場合、ベクトルは同一線上にあるためです。これは次のように表現されます。
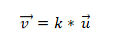
例1
ベクトルa =(10、5)とb =(6、3)があります。それらが同一直線上にあるかどうかを決定するために行列式理論が適用され、それは外積の同等性を確立する。そのように、あなたはしなければなりません:
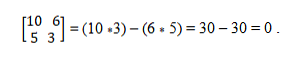
共線ベクトルシステム
共線ベクトルは、これらの方向と意味を使用してグラフィカルに表現されます。これらは、適用ポイントを通過する必要があることと、一定の縮尺または長さであるモジュールを考慮しています。.
共線ベクトル系は、力を表し、同じ方向に作用する、2つ以上のベクトルがオブジェクトまたはボディに作用するときに形成されます。.
たとえば、2つの共線力が物体に適用されている場合、これらの結果はそれらが作用する方向にのみ依存します。以下の3つのケースがあります。
反対方向の共線ベクトル
2つの共線ベクトルの結果は、これらの合計に等しくなります。
R =ΣF = F1 + F2.
例
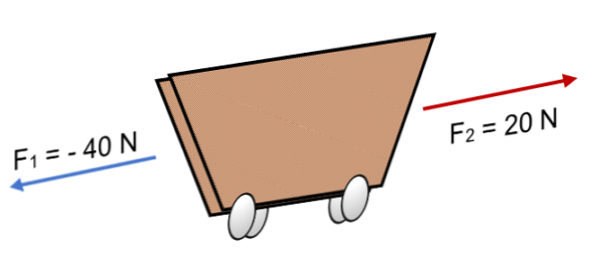
2つの力がカートに作用する場合F1 = 40 NおよびF2 (画像に示すように)反対方向に= 20 Nの場合、結果は
R =ΣF =( - 40 N)+ 20 N.
R = - 20 N.
同じ意味の共線ベクトル
合力の大きさは、共線ベクトルの合計に等しくなります。
R =ΣF = F1 + F2.
例
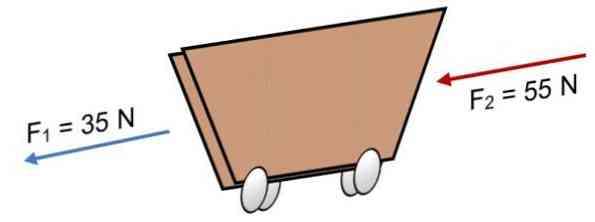
2つの力がカートに作用する場合F1 = 35 NおよびF2 = 55 N(画像に示すように)同じ方向では、結果は次のようになります。
R =ΣF = 35 N + 55 N.
R = 90 N.
正の結果は、共線ベクトルが左に向かって作用することを示しています.
大きさが等しく反対方向の共線ベクトル
2つの共線ベクトルの結果は、共線ベクトルの合計に等しくなります。
R =ΣF = F1 + F2.
力の大きさは同じだが反対方向であるため、一方が正になり、他方が負になります。2つの力を加算すると、結果はゼロになります。.
例
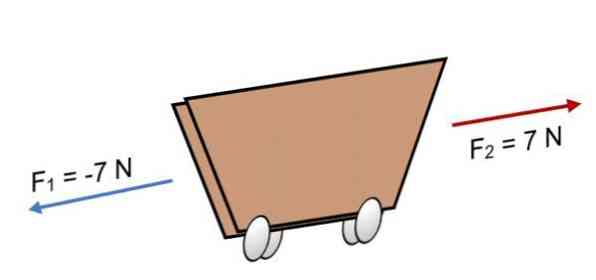
2つの力がカートに作用する場合F1 = -7 NとF2 = 7 N、大きさは同じだが反対方向(画像に示すように)、結果は次のとおりです。
R =ΣF =( - 7 N)+ 7 N.
R = 0.
結果は0に等しいので、それはベクトルが互いに釣り合っていることを意味します、そしてそれ故に、体は平衡状態にあるか、または静止しています(動かないでしょう).
共線ベクトルと同時ベクトルの違い
共線ベクトルは、同じ線上で同じ方向を向いていること、または線と平行であることを特徴としています。つまり、それらはベクトル直接平行線です。.
一方、並行ベクトルは、1つのポイントでインターセプトされるさまざまな行のアクションに含まれるために定義されます。.
言い換えれば、それらは、それらのモジュール、方向または方向にかかわらず、同じ原点または到着点を持ち、それらの間に角度を形成する。.
並行ベクトル系は、力の平行四辺形の方法および力の多角形の方法である数学的方法またはグラフによって解かれる。これらを通して、結果として得られるベクトルの値が決定され、それは身体が動く方向を示します.
基本的に、共線ベクトルと同時ベクトルの主な違いは、それらが作用する作用線です。つまり、共線ベクトルは同一線上で作用しますが、同時ベクトルは異なる方向に作用します。.
つまり、共線ベクトルは単一平面、 "X"または "Y"に作用します。同じ点から始めて、両方の面で同時に行動する.
共線ベクトルは、並列ベクトルとは異なり、互いに平行であるため、一点にありません。.
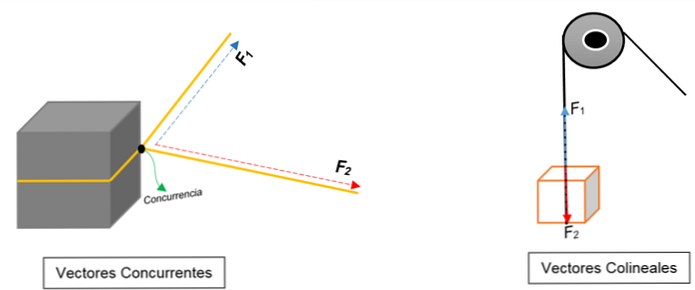
左の画像では、ブロックが見えます。それはロープで縛られ、結び目はそれを2つに分けます。異なる向きに異なる力で引っ張られると、ブロックは同じ方向に向かって移動します.
2つのベクトルは、それらのモジュール、方向、方向に関係なく、点(ブロック)内で一致するように表されます。.
代わりに、右の画像では箱を持ち上げる滑車が現れています。ロープは行動の線を表します。引っ張られると、2つの力(ベクトル)が作用します。1つの力(ブロックを登るとき)ともう1つの力(ブロックの重量をかける力)です。両方とも同じ方向ですが反対方向です。一点に同意しない.
参考文献
- Estalella、J. J.(1988)。ベクトル分析第1巻.
- Gupta、A.(s.f.)。 Tata McGraw-Hill教育.
- Jin Ho Kwak、S. H.(2015)。線形代数Springer Science&Businessメディア.
- Montiel、H。P.(2000)。技術バカロレアのための物理学1。パトリア編集グループ.
- Santiago Burbano de Ercilla、C。G.(2003)。一般物理学社説テバ.
- Sinha、K.(s.f.)。数学の教科書XII第2巻ラストギ出版物.


