アルキメデスの伝記、貢献および発明
シラキュースのアルキメデス シチリア島の古代都市シラキュース出身の数学者、物理学者、発明家、エンジニア、そしてギリシャの天文学者。彼の最も優れた貢献はアルキメデスの原理、呼気方法の開発、機械的方法または最初のプラネタリウムの創造です。.
現時点では、その貢献は当時の計算、物理学、幾何学、天文学の分野における重要な科学的進歩を意味していたので、それはユークリッドとアポロニオの隣の古代の数学の3つの最も重要な人物の1人のように考えられます。言い換えると、これは彼を人類の歴史の中で最も優れた科学者の一人にします.

彼の私生活についての詳細はほとんど知られていない - そして知られているものは信頼できない信頼性がある - が、彼の貢献は現在まで保存されている彼の作品と業績についての一連の書面の手紙のおかげで知られている。彼がその当時の友人や他の数学者と何年もの間続けてきた対応へ.
アルキメデスは彼の同時代の人々の注目を集めた彼の発明のおかげで彼の時代に有名でした。.
しかし、彼は唯一の本当に重要なことは数学であり、彼の発明は単に応用幾何学の娯楽の産物であると主張したと言われています。後世に、純粋な数学における彼の作品は彼の発明よりはるかに高く評価されています.
索引
- 1伝記
- 1.1トレーニング
- 1.2科学的な仕事
- 1.3シラキュースの対立
- 1.4死
- 2アルキメデスの科学的貢献
- 2.1アルキメデスの原理
- 2.2機械的方法
- 2.3レバーの法則の説明
- 2.4科学的実証のための呼気消耗方法の開発
- 2.5円の大きさ
- 2.6球と円柱の幾何学
- 3発明
- 3.1走行距離計
- 3.2最初のプラネタリウム
- 3.3アルキメデスネジ
- 3.4アルキメデスの爪
- 4参考文献
伝記
シラキュースのアルキメデスは、紀元前287年頃に生まれました。彼がシチリア島の主な港であると考えられていたシラキュース、今日のイタリアで生まれたと言うことができますが、彼の初期の頃についてはあまり多くの情報は知られていません。.
当時、シラキュースは、ギリシャの起源の入植者がイタリア半島の南部地域とシチリア島に住んでいた、いわゆるマグナグレシアを構成する都市の1つでした。.
アルキメデスの母についての既知の事実はありません。父親に関連して、これはフィディアスと呼ばれ、彼が天文学に専念していたことが知られています。彼の父親のこの情報は本の断片のおかげで知られています サンドカウンター, アルキメデスによって書かれた、彼は彼の父の名前に言及します.
ギリシャの哲学者で天文学者だったHeraklidesはアルキメデスが大好きで、彼についての伝記も書いています。しかし、その文書は保存されていないため、そこに含まれるすべての情報は不明です。.
一方、歴史家、哲学者、伝記作家のPlutarcoは、彼の著書 『Parallel Lives』で、アルキメデスは紀元前265年以来シラキュースで責任を負ってきたヒエロ2世と血縁関係にあると述べています。.
トレーニング
アルキメデスについて私たちが持っているわずかな情報の結果として、私たちは彼が彼の最初の訓練を受けた場所を確実に知りません.
しかし、様々な歴史学者は、アルキメデスがこの地域で最も重要なギリシャの文化と教育の中心地であったアレクサンドリアで研究した可能性が高いと判断しました。.
この仮定は、アルキメデスがおそらくアレクサンドリアで研究したことを示したギリシャの歴史家ディオドロ・シクロによって提供された情報によって支持されます。.
さらに、彼の作品の多くでアルキメデス自身がその仕事がアレクサンドリアに集中していた当時の他の科学者について言及しているので、彼は実際にその都市で発展したと考えることができる.
アルキメデスがアレクサンドリアで相互作用したと信じている人格の中には、キレネの地理学者、数学者、天文学者エラトステネス、そして数学者、天文学者コノン・デ・サノスがあります.
家族のやる気
一方、アルキメデスの父親が天文学者であったという事実は、彼がその後示した傾向に大きな影響を与えた可能性があります。科学.
アレクサンドリアで過ごした後、アルキメデスはシラキュースに戻ったと推定されています.
科学的な仕事
シラキュースに戻った後、アルキメデスはすぐに彼にこの都市の住民の間で一定の人気を獲得したさまざまなアーティファクトを考案し始めました。この時期に彼は完全に科学的研究に専念し、様々な発明を生み出し、彼の時代に非常に進んだいくつかの数学的概念を演繹しました。.
例えば、彼が立体曲線や平面図形の特性の研究に専念したとき、彼は後で開発された積分と微分計算に関連する概念を思い付きました.
また、アルキメデスは、球に関連する体積がそれを含む円柱のサイズの2倍に相当すると定義したものであり、レバーの法則についての彼の発見に基づいて複合プーリーを発明したものです。.
シラキュースの紛争
紀元前213年の間に、ローマの兵士たちはシラキュースの町に入り、彼らを降伏させるためにその入植者たちを取り囲みました。.
この行動は、第二次ポエニ戦争の枠組みの中で軍とギリシャの政治家マルコ・クラウディオ・マルセロによって導かれました。その後、それはシラキュースを征服することになったので、ローマの剣として知られていました.
2年間続いた紛争の最中に、シラキュースの住民は勇気と激しさでローマ人と戦いました、そしてアルキメデスはローマ人を倒すのを助けた道具と道具をつくることに彼自身を捧げたことを考えると.
最後に、マルコクラウディオマルセロはシラキュースの街を取った。アルキメデスの偉大な知的能力の前に、Marceloは彼らが傷つけられたり殺されたりしないように命じました。しかし、アルキメデスはローマの兵士の手によって殺されました.
死
アルキメデスは紀元前212年に亡くなりました。彼の死後130年以上、紀元前137年に、作家、政治家そして哲学者マルコ・ツリオ・キセロはローマの政権の地位を占め、アルキメデスの墓を見つけたかったです。.
Ciceroは正確な場所を示す人を見つけることができなかったため、この作業は簡単ではありませんでした。しかし、彼はやがてアグリジェントの扉の近くで、そして哀れな状態でそれを手に入れました。.
Ciceroは墓をきれいにし、アルキメデスがしばらく前に作った容積についての発見への参照として、それが円柱の内側の球で刻まれていることを発見しました。.
彼の死についてのバージョン
最初のバージョン
バージョンの1つは彼がローマの兵士によって近づかれたときアルキメデスが数学的問題を解決している最中であったと述べている。アルキメデスは問題を解決するためにしばらくの間彼に頼んだかもしれないと言われているので、兵士は彼を殺したでしょう.
第二版
2番目のバージョンは最初のバージョンと似ています。街の占領が起こったときにアルキメデスが数学の問題を解決していたと説明する.
ローマの兵士が自分の敷地内に入ってマルセロに会うように命じ、アルキメデスは自分が最初に取り組んでいた問題を解決しなければならないと答えました。兵士はこの反応の結果として動揺し、彼を殺しました.
第三版
この仮説はアルキメデスが彼の手に数学に典型的な道具の非常に多様性を持っていたことを示します。それから兵士は彼を見ました、そして、彼は彼が彼が彼を殺した貴重なアイテムを持っているかもしれないと思った.
第4版
このバージョンはアルキメデスが彼が勉強していた計画を熟考しながら地面近くでうずくまっていたことを例証します。どうやら、ローマの兵士が後ろから来た、そしてそれがアルキメデスであることに気づいていなかった、彼を撃った.
アルキメデスの科学的貢献
アルキメデスの原理
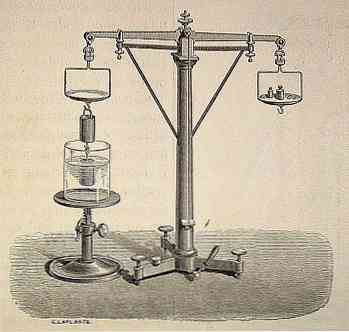
アルキメデスの原理は、現代科学によって古代の最も重要な遺産の1つと見なされています。.
歴史を通して、そして口頭で、アルキメデスが彼によって製造されるために送られた金の王冠が金だけで作られたかどうか見るように依頼された王ヒエロンのおかげで偶然彼の発見に来たことが報告されました純粋で他の金属を含んでいませんでした。私は王冠を破壊することなくこれを実行しなければなりませんでした.
アルキメデスがこの問題を解決する方法を瞑想している間、彼は風呂に入ることに決めました、そして、彼が浴槽に入るとき、彼は彼がそれに浸ったとき水が水平に上がると気づきました。.
このようにして、彼は「すべての物体が全体的にまたは部分的に流体(液体または気体)に浸されて、物体によって取り除かれた流体の重量に等しい上向きの推力を受ける」という科学原理を発見するでしょう。.
この原理は、流体がそれらに浸されたどんな物体にも上向きに押す力を発揮すること、そしてこの押し付け力の量は、その重さに関係なく、沈められた物体によって置き換えられた液体の重さに等しいということを意味します.
この原理の説明は浮選の現象を説明しており、その中にあります。 浮体に関する条約.
アルキメデスの原理は潜水艦、船、ライフガード、気球などの大量に使用される物体の浮遊のために後世に大いに応用されてきました。.
機械的方法
アルキメデスの科学への最も重要な貢献のもう一つは、幾何学的問題の推論と論証における純粋に機械的な、すなわち技術的な方法の包含であり、これは当面この種の問題を解決する前例のない方法を意味した。.
アルキメデスの文脈では、幾何学はもっぱら理論的な科学と考えられていました、そして、共通のことは純粋な数学がその原理が適用されることができる他の実用的な科学に向かって降りたということでした。.
このため、今日では科学分野としての力学の先駆けと見なされています。.
数学者が彼の友人Eratosthenesに新しい方法を公開している文章では、これが力学を通して数学の問題に取り組むことを可能にし、幾何学的定理の証明を既に立てておけば構築する方がいくぶん簡単であることを示しますあなたがそれについて少しの考えも持っていないならば、それにはいくつかの事前の実用的な知識があります.
アルキメデスによって行われたこの調査の新しい方法は、現代の科学的方法の発見と仮説の定式化の前段階になるでしょう。.
てこの法則の説明
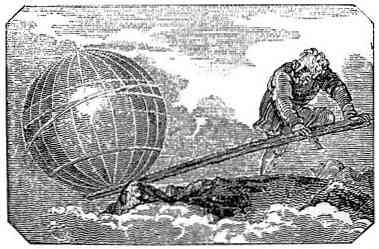
レバーはアルキメデスよりずっと以前から使用されていた単純な機械ですが、それは彼の論文でその動作を説明する原理を定式化した彼でした.
この法律の定式化において、アルキメデスは、その重さと支持点からの距離に応じて、2つの物体を置くときのレバーの異なる動作を説明する原則を確立します。.
このようにして、彼は、レバー上に位置する測定可能な(釣り合い可能な)2つの物体が、それらの重量に反比例する距離にあるときにバランスがとれていることを指摘しています。.
同様に、計り知れない体(測定不可能)はそうしますが、この法則はアルキメデスによって最初のタイプの体でのみ証明されました.
それはそれに従ってDositeoに向けられた手紙で説明するように、これは実際に置く力学の方法を通して発見されたので、レバーの原理のその定式化は機械的方法の適用の良い例です.
後で彼は幾何学の方法を使ってそれらを定式化した(理論的)。身体に関するこの実験から、重心の概念も切り離されました.
科学的実証のための呼気または吸尽法の開発
消耗は、面積が既知であることが意図されている別の図形上で、面積が既知の幾何学図形を刻印および外接によって近似することからなる幾何学において使用される方法である。.
アルキメデスはこのメソッドの作成者ではありませんでしたが、彼はそれを使ってPiの正確な値を計算することをうまく管理しながら、それを巧みに開発しました.
アルキメデスは、吐き出し法を使用して、直径1の円周に内接および外接する六角形を使用し、六角形の面積と円周の面積との差を不合理に減らします。.
これを行うために、前の図に示すように、彼は六角形を2等分して最大16辺のポリゴンを作成しました。.
このようにして、彼はpiの値(円の長さとその直径の間の関係)が3.14084507 ...と3.14285714 ...の間の値になるように指定するようになりました。 .
アルキメデスは、エラーマージンをかなり低くしてPiの値の計算を近似することができただけでなく、それが望ましいため、また、Piが非合理的な数であるため、徹底的にexuciónの方法を使用しました。この方法と得られた結果は無限小計算システム、そして後に現代の積分計算で発芽する基礎を築いた。.
円の大きさ
円の面積を決定するために、アルキメデスは円の内側にぴったり収まる正方形を描くことからなる方法を使用しました.
正方形の面積がその辺の合計であり、円の面積が大きいことを知って、彼は近似を得ることに取り組み始めました。これは、正方形を6面の多角形に置き換えてから、より複雑な多角形で作業することによって行いました。.
アルキメデスはパイの数の真剣な計算をすることにアプローチする歴史の中で最初の数学者でした.
球と円柱のジオメトリ
数学と物理学におけるアルキメデスの研究をまとめた9つの論文の中で、球と円柱の幾何学に関する2巻があります.
この研究は、半径の球の表面はその最大の円のそれの4倍であり、そして球の体積はそれが刻まれている円柱のそれの2/3であるという決定を扱う。.
発明
走行距離計
キロメートルとも呼ばれる、それはこの有名な男の発明でした.
この装置は、回転すると走行距離を計算することができる歯車を作動させるという車輪の原理に基づいて作られました。.
これと同じ原理に基づいて、アルキメデスは軍事用および民事用に数種類の走行距離計を設計しました。.
最初のプラネタリウム
Cicero、Ovid、Claudian、Marciano Capela、Casiodoro、Sexto Empirico、Lactantiusなどの多くの古典的な作家の証言に基づいて、多くの科学者はアルキメデスに最初の初歩的なプラネタリウムの創造を帰属させる.
それは惑星の動きを模倣することに成功した一連の「球」によって構成されるメカニズムです。これまでのところ、このメカニズムの詳細は不明です.
Ciceroによると、アルキメデスによって建てられたプラネタリウムは2つでした。そのうちの一つには、土地とその近くの様々な星座が描かれていました。.
もう1つは、1回の回転で、太陽、月、惑星は、実際の日に行ったのと同じ方法で、恒星に対して独自の独立した動きをしたことです。後者では、さらに、月の連続的な段階と食.
アルキメデスのネジ
アルキメデススクリューは、チューブまたはシリンダーを使用して、斜面を通って下から上に水を輸送するために使用される装置です。.
ギリシャの歴史家ディオドロによれば、この発明のおかげで、古代エジプトのナイル川沿いにある肥沃な土地の灌漑が容易になりました。伝統的な道具では、労働者を疲弊させる莫大な肉体的努力が必要だったからです。.
使用されるシリンダーは内部に同じ長さのスクリューを持ち、それは回転するレバーによって手動で駆動される回転運動を実行するプロペラまたはフィンのシステムを相互接続して維持する.
このようにして、らせんは何らかの物質を下から上へ押し上げ、一種の無限回路を形成します。.
アルキメデスの爪
アルキメデスの爪、あるいはそれが知られているような鉄の手は、この数学者によって生み出された最も恐ろしい戦争の武器の1つであり、シチリアのローマ侵略の防衛にとって最も重要なものとなった。.
Drexel大学教授Chris Rorres(数学科)とHarry Harris(土木工学科)が行った研究によると、それはレバーにつかみフックが付いている大きなレバーでしたそれから掛けられた鎖によって.
レバーを通してフックが操作されて敵の船に落ち、目的はそれを引っ掛けてそれを解放するとそれが完全にひっくり返ったり、海岸の岩に当たったりすることができる程度までそれを上げることでした。.
RorresとHarrisはシンポジウム「古代の機械と並外れた構造」(2001年)で、「手に負えない戦争機械:アルキメデスの鉄の手の製作と運用」と題したこの遺物のミニチュア表現を発表しました。
この作品の実現のために、彼らは古代の歴史家Polibio、PlutarcoとTito Livioの議論に頼りました.
参考文献
- ASSIS、A。(2008)。アルキメデス、重心、そして力学の第一法則[オンライン]。 2017年6月10日にbourabai.ruにアクセス.
- DIJKSTERHUIS、E.(1956)。アルキメデス[オンライン]。 2015年6月9日にワールドワイドウェブ上でアクセスされている:books.google.co.ve/books.
- MOLINA、A.(2008)。シラキュースのアルキメデスの研究方法:直感、力学そして尽き[オンライン]。 2017年6月10日にワールドワイドウェブプロダクションサイエンティカ.luz.eduでアクセス.
- O'CONNOR、J.&ROBERTSON、R.(1999)。シラキュースのアルキメデス[オンライン]。 history.mcs.st-and.ac.ukで2017年6月9日にアクセス.
- PARRA、E.(2009)。アルキメデス:彼の人生、作品、そして現代数学への貢献[オンライン]。 2017年6月9日にlfunes.uniandes.edu.coで取得.
- QUINN、L.(2005)。シラキュースのアルキメデス[オンライン]。 2017年6月9日、math.ucdenver.eduでアクセス.
- RORRES、C.&HARRIS、H.(2001)。手ごわい戦争機械:アルキメデスの鉄の手の製作と操作[オンライン]。 2017年6月10日、cs.drexel.eduで取得しました.
- VITE、L.(2014)。アルキメデスの原理[オンライン]。 2017年6月10日にrepository.uaeh.edu.mxで取得しました.


