毛細管特性と水中での例
の 毛細管 重力に反してもそれらが管状の穴または多孔性表面を通って動くことを可能にするのは液体の特性である。そのためには、液体分子に関連する2つの力のバランスと調整が必要です。これら二つを持つことは表面張力と呼ばれる物理的な反射.
液体は、チューブの内壁またはそれが移動する材料の細孔を濡らすことができる必要がある。これは、付着力(毛細管の液壁)が分子間凝集力よりも大きいときに起こる。その結果、液体分子はそれらの間よりも材料(ガラス、紙など)の原子とのより強い相互作用を作り出す。.
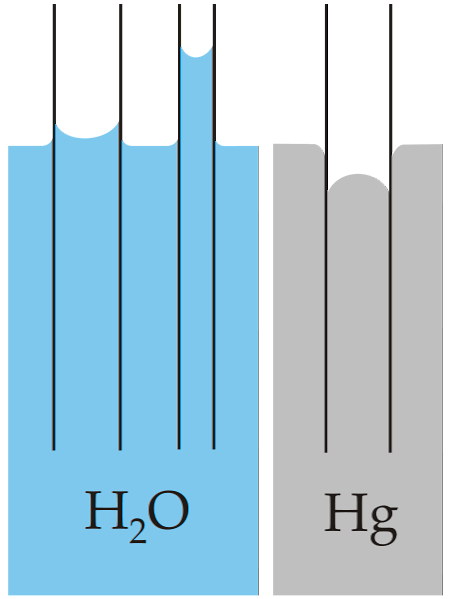
毛細管現象の典型的な例は、2つの非常に異なる液体(水と水銀)に対するこの特性の比較に示されています。.
上の画像は、水がチューブの壁を通って上昇することを示しています。これは、それがより高い付着力を持っていることを意味します。その反対は水銀で起こります、なぜならその凝集力、金属結合力はそれがガラスを濡らすのを防ぐからです.
このため、水は凹面のメニスカスを形成し、水銀は凸面のメニスカス(ドーム型)を形成します。また、チューブの半径または液体が移動する部分の半径が小さいほど、移動した高さまたは距離は大きくなります(両方のチューブの水柱の高さを比較してください)。.
索引
- 1毛細管現象の特徴
- 1.1 - 液体の表面
- 1.2 - 身長
- 1.3 - 表面張力
- 液体が上昇する毛細管または細孔の1.4−ラジオ
- 1.5 - 接触角(θ)
- 2水の毛管現象
- 2.1植物について
- 3参考文献
毛細管現象の特徴
-液体の表面
毛細管中の液体の表面、例えば水は凹面である。つまり、メニスカスは凹面です。この状況は、管の壁の近くの水分子に及ぼされる力の合力がこれに向けられるために起こります。.
全てのメニスカスには接触角(θ)があり、これは接触点で液体の表面に接する線で毛細管の壁を形成する角度である。.
接着力と凝集力
毛管壁への液体の付着力が分子間凝集力よりも優勢である場合、そのとき角度はθである。 < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
一滴の水がきれいなガラスの表面に置かれるとき、水はガラスの上に広がるので、θ= 0とcosθ= 1.
分子間凝集力が、例えば水銀中で、毛細管の液壁接着強度を上回る場合、メニスカスは凸状になり、角度θは> 90°の値を有することになる。水銀は毛細管壁を濡らさず、したがってその内壁を通って下降する。.
一滴の水銀がきれいなガラスの表面に置かれるとき、一滴はその形状と角度θ=140ºを維持します.
-身長
水は毛細管を通って上昇して高さ(h)に達します。そこでは、水柱の重量が分子間凝集力の垂直成分を補償します。.
水が上がるにつれて、表面張力が働いていても重力が上がるのを止めるようになるでしょう。.
これが起こると、分子は内壁を「登り」続けることができず、すべての物理的な力が均等化されます。一方では水の上昇を促進する力があり、他方ではそれを押し下げるあなた自身の体重.
ジュリンの法則
これは数学的には次のように書くことができます。
2πrTHcosθ=ρgπr2時間
式の左辺が表面張力に依存する場合、その大きさは凝集力または分子間力にも関係します。 Cosθは接触角を表し、rは液体が上がる穴の半径を表します.
そして方程式の右辺には、高さh、重力g、そして液体の密度があります。それは水だろう.
クリアしてから
h =(2γcosθ/ρgr)
この公式はJurinの法則として知られており、液柱の重さと毛細管現象による上昇力のバランスが取れている場合、毛細管内で液柱が到達する高さを定義します。.
-表面張力
酸素原子の電気陰性度とその分子構造により、水は双極性分子です。これは、酸素が位置する水分子の部分を負に帯電させる一方、2個の水素原子を含む水分子の部分は正に帯電する。.
これにより、液体内の分子は複数の水素結合を介して相互作用し、それらを結合させます。しかしながら、界面水:空気(表面)中にある水分子は、液体副鼻腔の分子による正味の引力を受け、空気分子との弱い引力によって補償されない。.
したがって、界面の水分子は界面から水分子を除去する傾向がある引力を受ける。つまり、下部の分子で形成された水素ブリッジは、表面にあるものを引きずります。このように、表面張力は水の表面を減らすことを目的としています:空気界面.
hとの関係
ジュリンの法則の方程式を見ると、hはγに正比例することがわかります。したがって、液体の表面張力が大きいほど、材料の毛細管または細孔を通って上昇する高さが大きくなります。.
したがって、異なる表面張力を有する2つの液体AおよびBについて、最も高い表面張力を有する液体がより高い高さまで上昇することが予想され得る。.
この点から、高い表面張力が液体の毛細管特性を定義する最も重要な特性であると結論付けることができます。.
-液体が上がる毛細管または細孔の半径
ジュリンの法則の観察は、毛細管または孔の中の液体が到達する高さはその半径に反比例することを示している.
したがって、半径が小さいほど、毛管現象によって液柱が到達する高さは大きくなります。これは水が水銀と比較される画像で直接見ることができます.
半径0.05 mmのガラス管では、毛管現象による水柱は30 cmの高さに達します。吸引圧1.5 x 10、半径1μmのキャピラリーチューブ内3 hPa(1.5気圧に等しい)は、14から15mの水柱の高さの計算に対応する。.
これは、それ自体が数回回転するストローで起こることと非常によく似ています。液体を吸うことによって、液体を口に上げる原因となる圧力差が発生します.
毛細管の半径はある限度を超えて減少させることはできないので、毛細管現象によって達成される柱の最大高さ値は理論的である。.
ポアズイユの法則
これは、実際の液体の流れが次の式で与えられることを証明します。
Q =(πr)4/8μm)ΔP
ここで、Qは液体の流れ、ηはその粘度、lの長さ、そしてΔPは圧力差です。.
毛細管の半径を小さくすると、毛細管現象が達する液体の柱の高さは無限に大きくなるはずです。しかし、Poiseuille氏は、半径を小さくするとその毛細管を通る液体の流れも減少することを指摘している.
さらに、実際の液体の流れに対抗する抵抗の尺度である粘度は、液体の流れをさらに減少させるでしょう。.
-接触角(θ)
cosθの値が大きいほど、Jurinの法則によって示されるように、毛管現象による水柱の高さが高くなります。.
θが小さく、ゼロ(0)に近づくと、cosθは= 1になるため、値hは最大になります。反対に、θが90°に等しい場合、cosθ= 0でh = 0の値.
凸面メニスカスの場合のように、θの値が90°より大きいと、液体は毛細管現象によって上昇せず、(水銀で起こるように)下降する傾向があります。.
水毛細管現象
水は72.75N / mの表面張力値を有し、以下の液体の表面張力の値と比較して比較的高い。
-アセトン:22.75 N / m
-エチルアルコール:22.75N / m
-ヘキサン:18.43 N / m
-メタノール:22.61 N / m.
それゆえ、水は例外的な表面張力を持ち、それは植物による水と栄養素の吸収に非常に必要な毛細管現象の発達に有利に働きます。.
植物について

毛細管現象は植物の木部による樹液の上昇のための重要なメカニズムであるが、樹液を木の葉に到達させることはそれだけでは不十分である。.
蒸散または蒸発は、植物の木部による樹液の上昇における重要なメカニズムである。葉は蒸発によって水分を失い、水分子の量を減少させ、それが毛細管(木部)に存在する水分子の引き付けを引き起こします。.
水分子は互いに独立して作用するのではなく、ファンデルワールス力によって相互作用し、それが植物の毛細管によって葉の方へ上昇するようにそれらを上昇させる.
これらのメカニズムに加えて、植物は浸透によって土壌から水分を吸収し、根に発生した陽圧が植物の毛細管を通って水の上昇を開始することに注意する必要があります。.
参考文献
- GarcíaFranco A.(2010)。表面的な現象取得元:sc.ehu.es
- 表面現象表面張力と毛管現象[PDF]取得元:ugr.es
- ウィキペディア(2018)。毛細管現象取得元:en.wikipedia.org
- Risvhan T.(s.f.)植物の毛細管現象。から取得しました:academia.edu
- Helmenstine、Anne Marie、Ph.D. (2018年12月22日)。毛管作用:定義と例以下から取得しました:thoughtco.com
- エレンエリスM.(2018)。水の毛管作用:定義と例勉強します。取得元:study.com
- ScienceStruckスタッフ(2017年7月16日)毛細管作用の概念と意味を説明する例。以下から取得しました:sciencestruck.com


