七角形プリズムの特徴と体積の計算方法

A 七角柱 その名前が示すように、2つの幾何学的定義を含む幾何学的図形です。プリズムと七角形.

「プリズム」とは、等しい平行多角形である2つの基底によって制限される幾何学図形であり、それらの側面は平行四辺形です。.

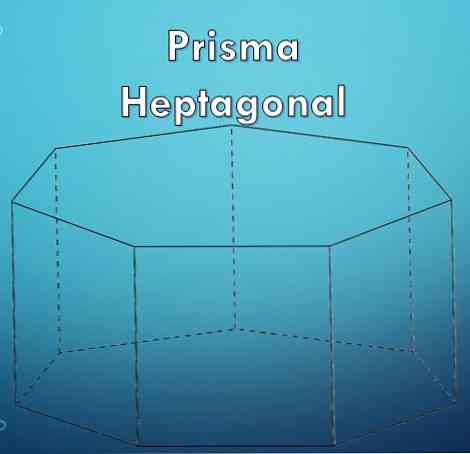
「七角形」は、7つの辺によって形成される多角形です。七角形は多角形なので、規則的または不規則的かもしれません.

多角形のすべての辺の長さが同じで、その内角が同じ大きさであれば、多角形は規則的であると言われます。これらは正三角形とも呼ばれます。さもなければそれは多角形が不規則であると言われます.

七角柱の特性

以下は、そのような七角柱を持つ特定の機能です。その構造、その基部の特性、そのすべての面の面積およびその容積.

七角柱を作成するには、2つの七角形が必要です。これは、底辺と7つの平行四辺形になります。七角形の両側に1つずつあります。.

七角形を描くことから始めて、それからそれぞれの頂点から来る同じ長さの7本の垂直線を描きます.

最後に別の七角形が描かれ、その頂点が前のステップで描かれた線の終点と一致するようになります。.

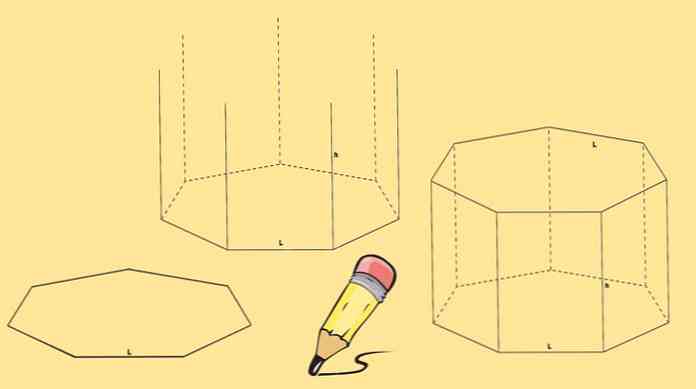
上に描かれた七角柱はまっすぐな七角柱と呼ばれます。しかし、次の図のような斜めの七角柱もあります。.

それらの底は七角形であるので、それらは対角数がD = nx（n-3）/ 2であることを遵守します。ここで、 "n"は多角形の辺の数です。この場合、D = 7×4/2 = 14となります。.

また、すべての七角形（規則的または不規則的）の内角の合計が900°であることもわかります。これは次の画像で確認できます。.

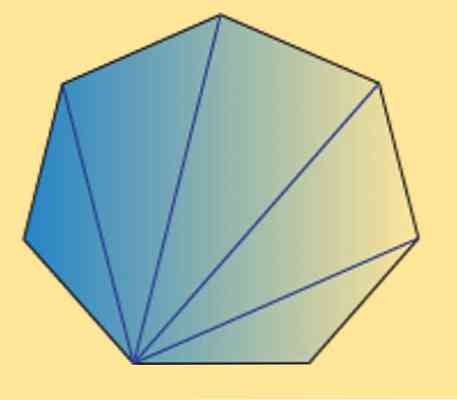
ご覧のとおり、5つの内部三角形があり、三角形の内角の合計を使用すると180ºになります。これにより、望ましい結果が得られます。.

底辺が2つの七角形で、側面が7つの平行四辺形であるため、七角柱の作成に必要な面積は2xH + 7xPになります。ここで、「H」は各七角形の面積、「P」は各平行四辺形の面積.

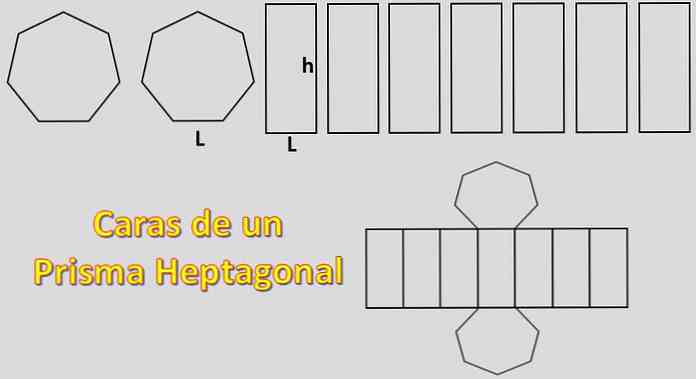
この場合、正七角形の面積が計算されます。そのためには、apothemaの定義を知ることが重要です。.

神格は、正多角形の中心からその辺のいずれかの中点に向かう垂線です。.

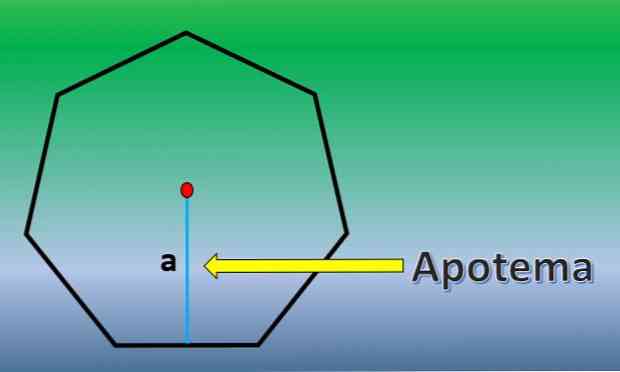
一旦薬局が知られると、七角形の面積はＨ＝７×Ｌ×ａ／２であり、ここで「Ｌ」は各辺の長さであり、「ａ」は薬局の長さである。.

平行四辺形の面積は計算が簡単で、P = Lxhとして定義されます。ここで、 "L"は七角形の辺の長さと同じで、 "h"はプリズムの高さです。.

結論として、七角形プリズムを作るために必要な材料の量（通常の底辺で）は7xLxa + 7xLxh、すなわち7xL（a + h）です。.

底辺の面積とプリズムの高さが分かれば、体積は（底辺の面積）x（高さ）として定義されます。.

七角形プリズムの場合（正則底面を有する）、その体積はＶ＝７×Ｌ×ａ／ｈ／２である。 V = Pxaxh / 2と書くこともできます。ここで、 "P"は正七角形の周囲長です。.

Billstein、R.、Libeskind、S.、＆Lott、J. W.（2013）. 数学：基礎教育教師のための問題解決アプローチ. ロペス・マテオス.
Fregoso、R. S.、＆Carrera、S. A.（2005）. 数学3. プログレソ編集長.
Gallardo、G.、＆Pilar、P. M.（2005）. 数学6. プログレソ編集長.
Gutiérrez、C。T.、およびCisneros、M。P.（2005）. 第3数学コース. プログレソ編集長.
Kinsey、L.、＆Moore、T. E.（2006）. 対称性、形状および空間：幾何学による数学入門 （イラスト、再版）。 Springer Science＆Businessメディア.
Mitchell、C.（1999）. まばゆいばかりの数学ラインデザイン （イラスト編）。スコラスティックインク.
R.、M。P.（2005）. 私は6º描く. プログレソ編集長.